All of the solutions to Ax=b

It should be simple right? Well, there are 7 different possible cases, and only 3 have simple solutions. Lets summarize.

Summary

We study

$$Ax = b$$

where $A \in \mathbb{C}^{m\times n}$, $x \in \mathbb{C}^n$ and $b \in \mathbb{C}^{b}$.

We will also use the adjoint $A^* \in \mathbb{C}^{n \times m}$ of $A$.

A few useful properties:

1. If, and only if, $b \in R(A)$, there exists a solution $x$.
2. If $b \not \in R(A)$ we are interested in finding a solution to $b_r$ which minimises the residual, $\|Ax - b\|$.
3. If there are linearly independent columns, $A$ must be tall, and admits the left inverse $A^+ = (A^* A)^{-1}A^*$
4. If there are linearly independent rows, $A$ must be fat, and admits the right inverse $A^+ = A^* (A A^*)^{-1}$.

	$b \in R(A) \implies$ solution exists	$b\not \in R(A)\implies$ solution does not exists
indep. cols: $N(A) = \{0\}$ (tall)	unique: $x = A^+ b = (A^* A)^{-1} A^* b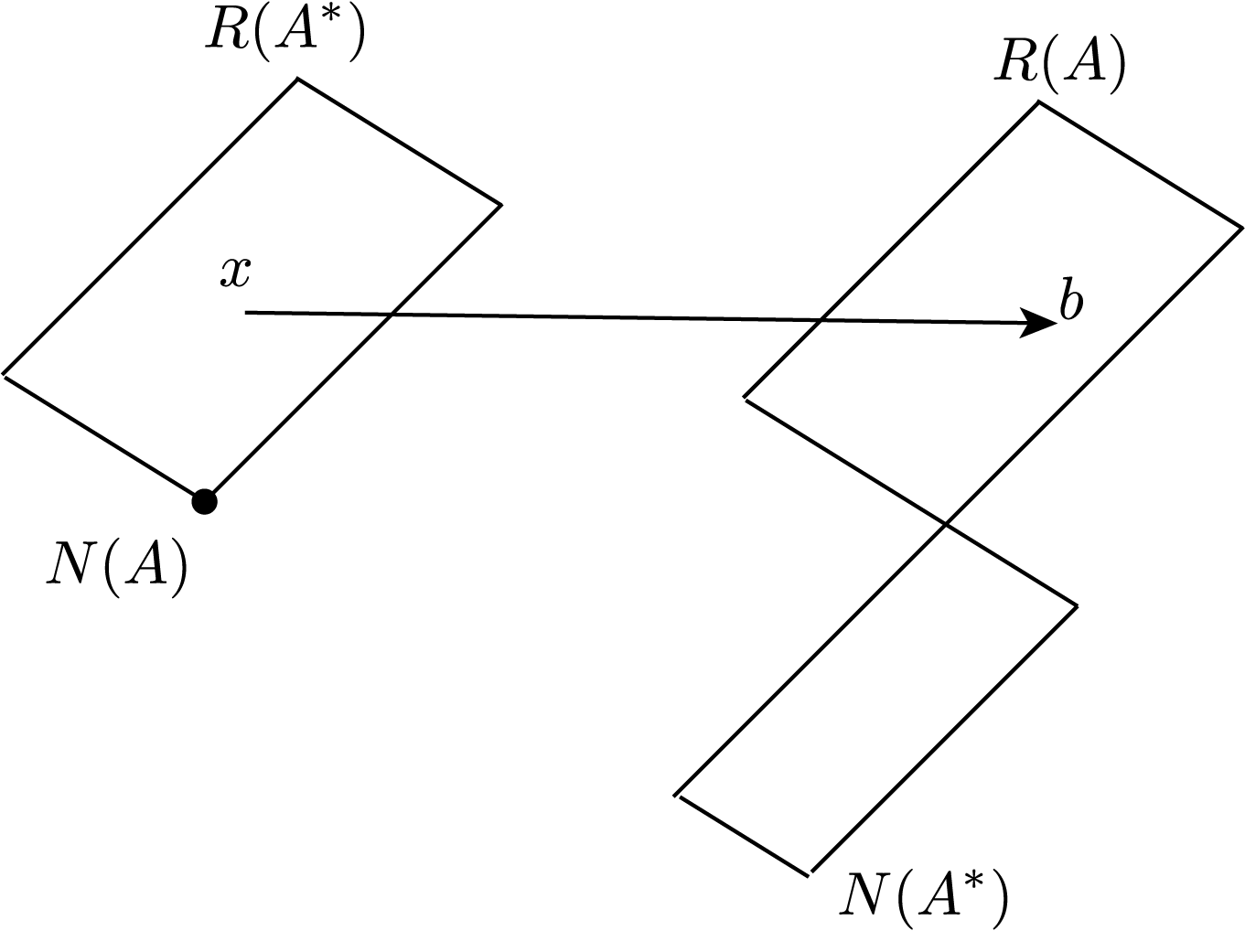$	least squares: $\tilde x = A^+ b = (A^* A)^{-1} A^* b$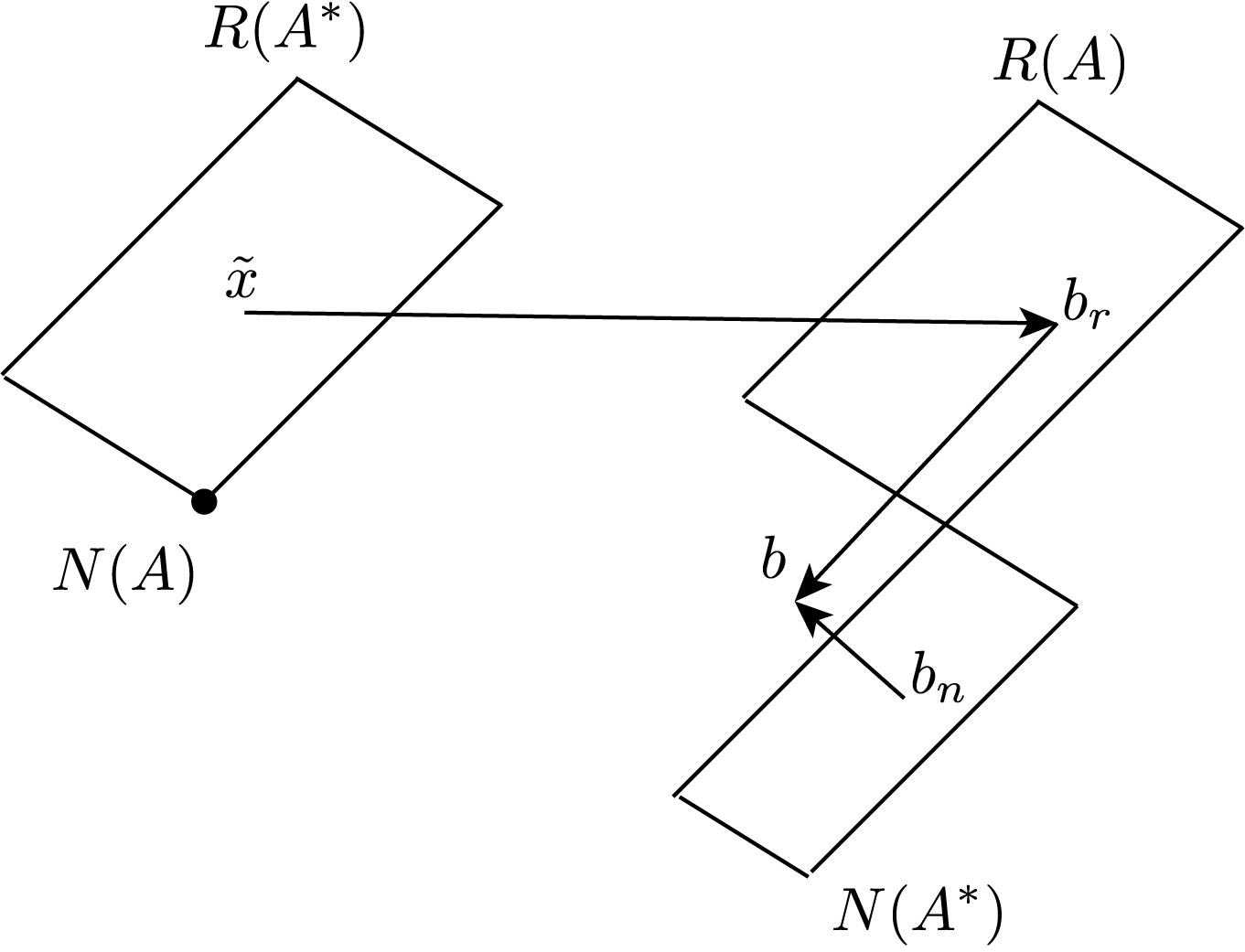
indep. rows: $N(A^*) = \{0\}$ (fat)	non-unique: $x = x_r + x_n$, and smallest sol: $x_r = A^+ b = A^* (A A^*)^{-1} b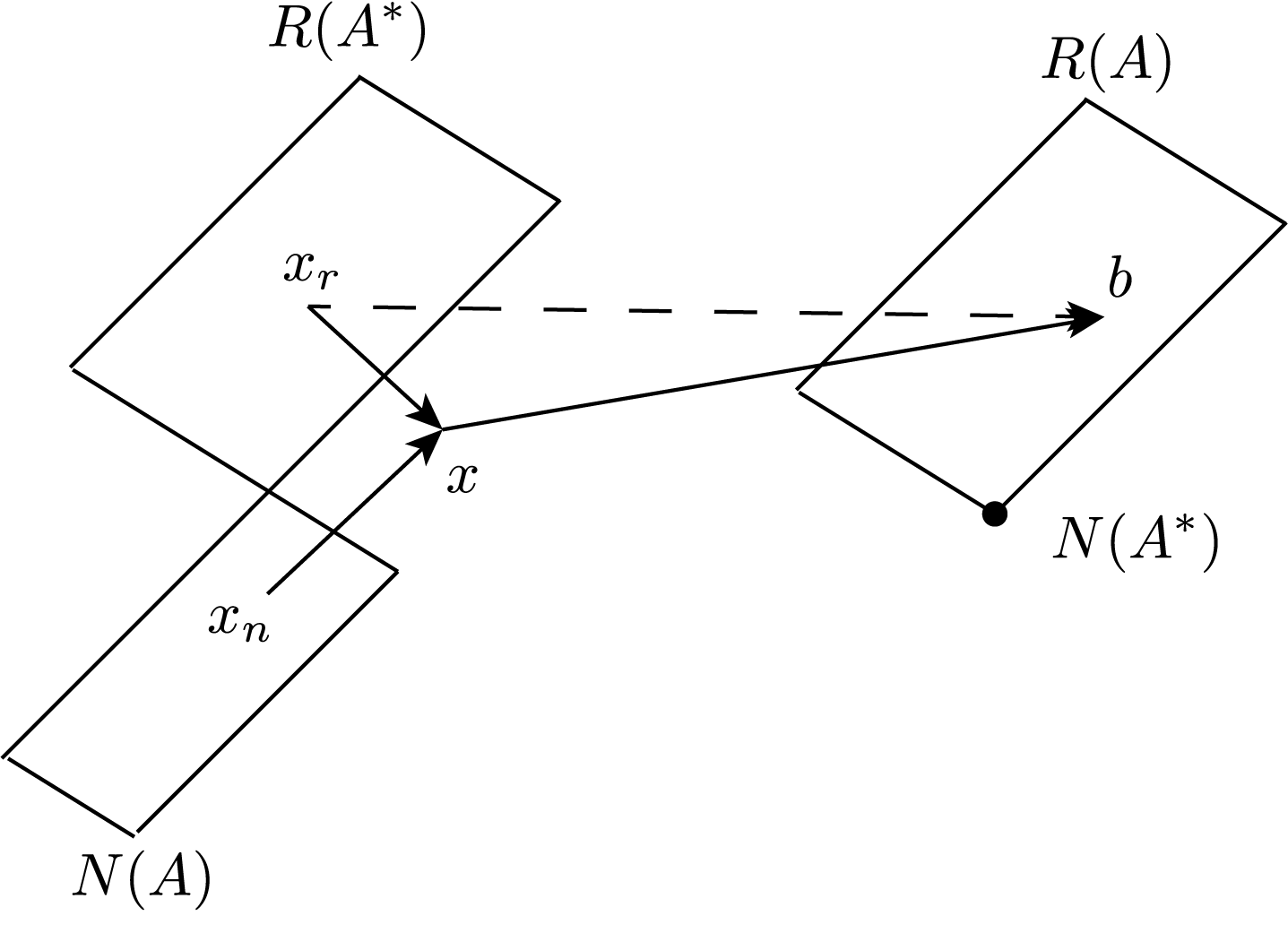$	Impossible Case (by rank-nullity)
dep. cols: $N(A) \neq \{0\}$ (tall)	solution not unique	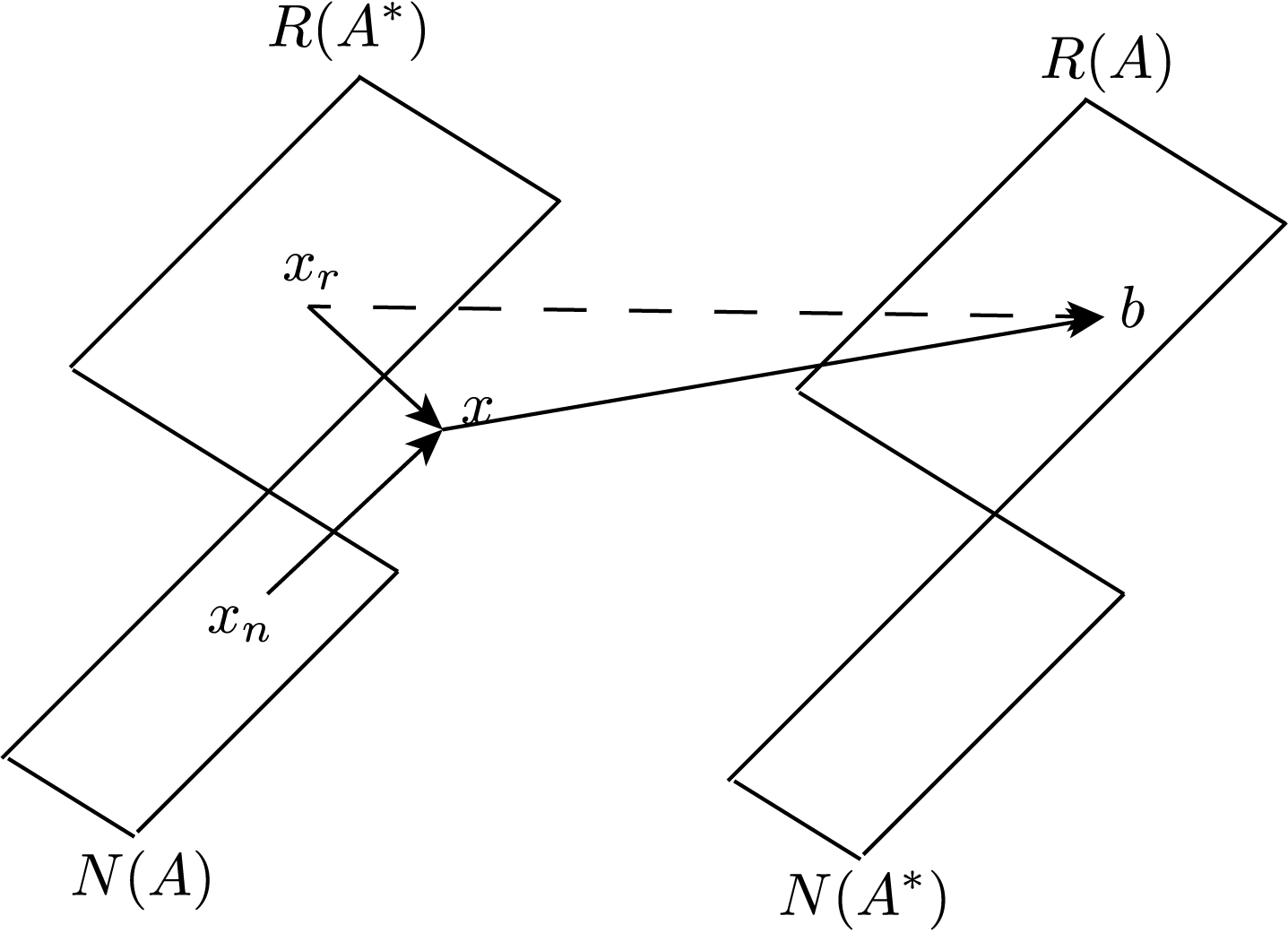no solution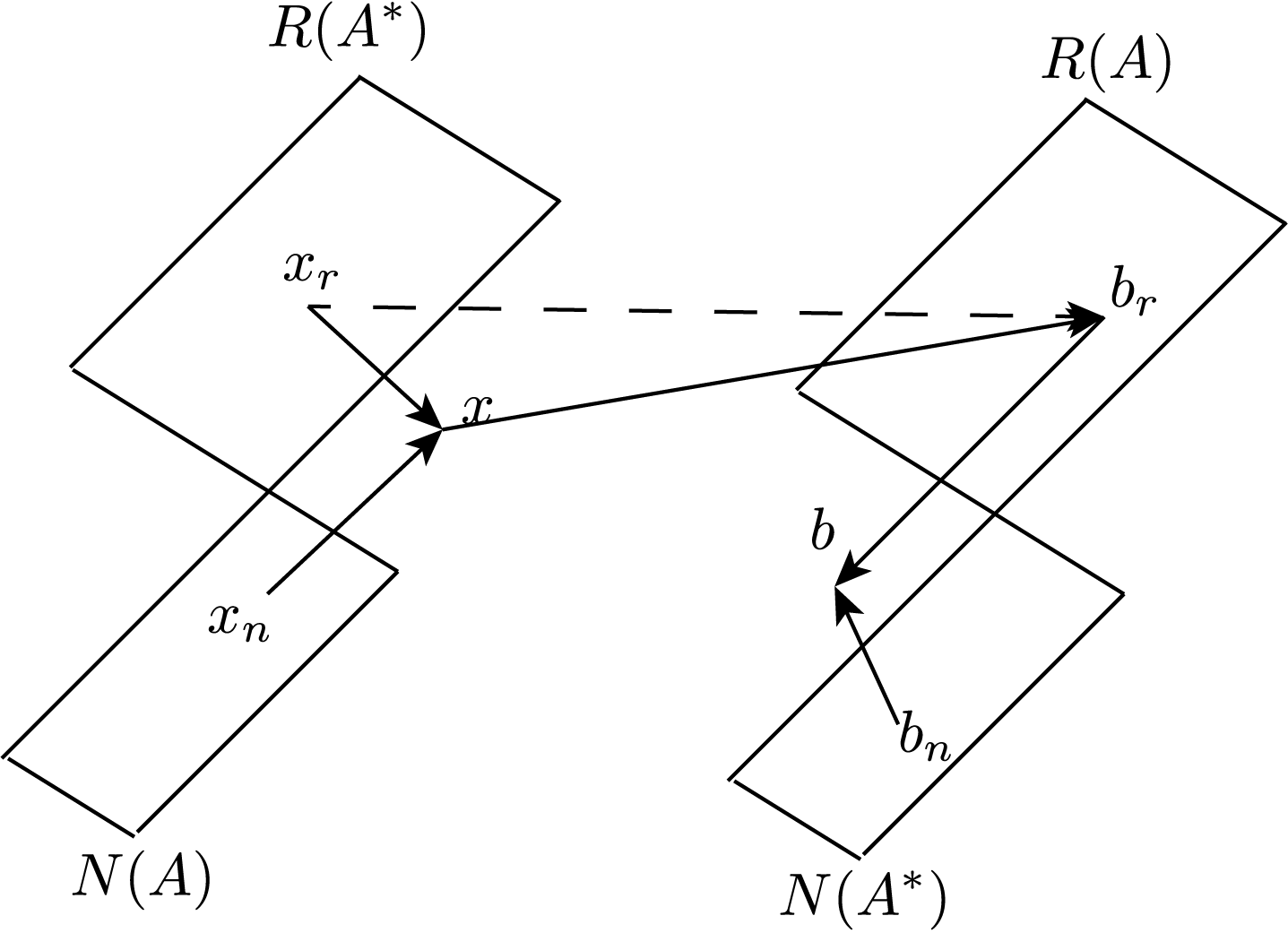
dep. rows: $N(A^*) \neq \{0\}$ (fat)	(same as above) solution not unique	(same as above) no solution

Left and Right Inverses

Following Boyd’s textbook on linear algebra, we define

1. The left inverse $X$ of a matrix $A$ is any martix that satisfies $X A = I$.
2. The right inverse $Y$ of a matrix $A$ is any matrix that satisfies $A Y = I$.

These have the following useful properties (proofs are simple, and I refer you to Boyd’s book, Ch 11):

1. The left inverse exists iff and only if the columns of $A$ are linearly independent.
2. A matrix can only have a left inverse if it is tall (or square).
3. If a matrix $A$ has left inverse $X$, then a solution to $Ax = b$ is $x = X b$.
4. A left invertible matrix $A$ has left inverse $X = (A^*A)^{-1}A^*$.
5. Left inverses are, in general, not unique.

Similarly, we can take the transpose of the above claims:

1. The right inverse exists iff and only if the rows of $A$ are linearly independent.
2. A matrix can only have a right inverse if it is fat (or square).
3. If a matrix $A$ has right inverse $Y$, then a solution to $Ax = b$ is $x = Y b$.
4. A right invertible matrix $A$ has right inverse $Y = A (AA^*)^{-1}$.
5. Right inverses are, in general, not unique.

Then suppose a matrix is both left and right invertible. Then the left and right inverses are equal and unique!

$$XA = I, \quad \text{ and } \quad AY = I\\ \implies X = X (AY) = (XA) Y = Y$$

Thus the inverse of a matrix $A$, if it exists, is $A^{-1} \triangleq X = Y$.

Notice that this only makes sense for square matrices, since for the left inverse to exist it must be tall, and for the right inverse to exist it must be fat. Thus, $A$ must be square.

The two special inverses $X = (A^*A)^{-1}A^*$ or $Y = A (AA^*)^{-1}$ require the matrices $(A^*A)$ or $(AA^*)$ to be invertible. This is always possible for left/right invertible matrices $A$, ie, if they have either linearly independent columns or rows.

But what about if this is not the case? We can use the Moore-Penrose Psuedo-Inverse, which is any matrix $A^+$ that satisfies the following four properties:

1. $$AA^+A = A$$
2. $$A^+ A A^+ = A^+$$
3. $$(AA^+)^* = AA^+$$
4. $$(A^+A)^* = A^+A$$

The psuedo inverse always exists, and is always unique. If $A$ is left or right invertible, the psuedo-inverse is the left or right inverse. If $A$ is invertible, the psuedo inverse is the inverse of $A$. This makes it a powerful abstraction of inverses, but you need to be careful: $A^+ A \neq I$ in general.

Solutions of simple cases

todo, proofs of each of the three simple cases above.

Solutions of other cases, using Singular Value Decomposition

todo.